昨天跟朋友讨论游戏开发的时候聊到了这个话题。
定义#
攻击速度(频率)和攻击间隔#
「攻击速度(Attack Speed)」:指单位时间内进行攻击的快慢程度。
通常以单位时间内执行的 攻击次数 来衡量,从这个角度来看,一般可以等价于「攻击频率(Attack Frequency)」;不过在我们所熟知的一些语境中,攻击速度 的叫法往往会比 攻击频率 更常见一点。
较高的 攻击速度 通常意味着 单位时间内进行更多的攻击。
「攻击间隔(Attack Interval)」:指两次连续攻击之间的时间间隔。
在一些游戏中(如泰拉瑞亚等)也被称为「使用时间(Use Time)」,即完成一次(攻击)动作所需使用(花掉,cost)的时间。
二者乍一听好像是同一个概念(同样可以用来描述攻击的快慢),只是说法不同。
但实际上并不是这样,其实在本质上,两者之间也是完全不同的东西。
举个例子,我们说在某个游戏中「加攻速」,一般情况下指的是直接增加 攻击速度;
然而,在另一些游戏里(如 Dota 2 中的基本攻击间隔 BAT),存在游戏内部机制能够缩减 攻击间隔 以达成更频繁地攻击的目的。
总的来说:
攻击速度强调在单位时间内进行攻击动作的 频繁程度。攻击间隔强调在连续两次攻击动作之间所需(且必然存在)的 时间间隔。
如果把对 攻击间隔 的描述换一个说法:进行 一次 完整攻击的周期 T,称为 攻击间隔。
将「一次完整攻击」作为参考标的,则有:
$$
\text{攻击频率(攻击速度)} f = \frac{1}{\text{攻击间隔} T}
$$
可以轻易发现 攻击速度 和 攻击间隔 实际上是倒数关系:攻击速度越高,则攻击间隔越短;反之亦然。
攻击次数(频次)#
此时可以从外部引入其他变量来进一步描述。
「战斗总时长(TTK,Time To Kill)」:击败敌人所需的全部时间(在此期间视为保持匀速攻击)。
「攻击频次(Attack Count)」:指在 某一段时间 内执行的攻击动作的数量。
为了防止和 攻击频率(即 攻击速度)混淆,我们这里就称之为 攻击次数。
$$
\text{攻击频率(攻击速度)} f = \frac{\text{攻击次数} n}{\text{战斗总时长} \tau}
$$
最终可得游戏内与攻速相关的各种物理量之间的全部关系: $$ \text{攻击频率(攻击速度)} f = \frac{1}{\text{攻击间隔} T} = \frac{\text{攻击次数} n}{\text{战斗总时长} \tau} $$
实际用途#
基础建模#
假设一个最简单的模型:
一次普通攻击(俗称「平 A」),在游戏中的具体效果呈现为给 攻击目标 造成一定量的伤害。
当任意一方 生命值(俗称「血量」)归零(≤ 0)时,战斗结束。
- 我方战败,此处不讨论,因为可以直接视为「游戏失败(Game Over)」另行处理。
- 敌方战败(且:与此同时,我方存活),则可以根据以上条件计算出我方的战损。
如何将双方的数值计算联立起来?
当然需要找到一个共享的数值,显然就是本次作战的全部耗时——「战斗总时长(TTK,Time To Kill)」。
为了简化模型,暂且将战斗双方的 攻击速度(即 攻击频率,等价于 1 / 攻击间隔)视为相同的固定值。且有:
$$
\text{战斗总时长} \tau = \text{我方攻击次数} n_1 \times \text{我方攻击间隔} T_1
$$
已经确定 攻击间隔 为固定值(常量),那么如何确定我方 攻击次数 呢?
很简单,Time To Kill(打到死):
$$
\text{我方攻击次数} n_1 = \lceil \frac{\text{敌方总血量} HP_2}{\text{我方单次攻击伤害} DPS_1} \rceil \tag{公式1}
$$
至于为什么是向上取整,因为如果敌方剩一点血皮没死,肯定不能让他苟住继续作妖;
你还要补刀,这次「补刀」显然得是一次完整攻击。
这里的「DPS」严格上说是错误的, 因为这里的值实际上代表 单次攻击能够造成的伤害。
而真正的 DPS 是 Damage Per Second 每秒造成伤害,与攻击间隔(而不是攻击次数)有关。
这里只是借用这个习惯叫法,MMO 里还常常有把 DPS 视作「总共造成的所有伤害」的约定俗成呢。
别问,问就是我缩写的其实是「Damage Per Single-attack」。
敌方明显应该共享这个战斗总时长,因此有: $$ \text{敌方攻击次数} n_2 \times \text{敌方攻击间隔} T_2 = \text{战斗总时长} \tau = \text{我方攻击次数} n_1 \times \text{我方攻击间隔} T_1 $$
约掉双方相等的固定值常量 攻击间隔,则双方 攻击次数 相等;
再代入 公式1(我方 攻击次数 一式)则有:
$$
\text{敌方攻击次数} n_2 = \text{我方攻击次数} n_1 = \lceil \frac{\text{敌方总血量} HP_2}{\text{我方单次攻击伤害} DPS_1} \rceil \tag{公式2}
$$
那么战损——即在本场战斗中会损失掉的 生命值 为:
$$
\text{我方战损} HP_1 = \text{敌方单次攻击伤害} DPS_2 \times \text{敌方攻击次数} n_2
$$
代入 公式2(敌方 攻击次数 一式)可得出我方本场战损为:
$$
\text{我方战损} HP_1 = \text{敌方单次攻击伤害} DPS_2 \times \lceil \frac{\text{敌方总血量} HP_2}{\text{我方单次攻击伤害} DPS_1} \rceil
$$
引入攻速#
上面的讨论仅在「双方攻击速度相等」的条件下成立,如果要引入不同的攻速变化呢?
通过 攻击间隔 和 攻击频率 之间的倒数关系容易想到:
$$
\frac{\text{我方攻击次数} n_1}{\text{我方攻击频率(攻击速度)} f_1} = \text{战斗总时长} \tau = \frac{\text{敌方攻击次数} n_2}{\text{敌方攻击频率(攻击速度)} f_2}
$$
稍作变换可得: $$ \text{敌方攻击次数} n_2 = \lfloor \frac{\text{敌方攻击频率(攻击速度)} f_2}{\text{我方攻击频率(攻击速度)} f_1} \times \text{我方攻击次数} n_1 \rfloor $$ 这里为什么又要向下取整呢?因为当攻速快的那方的最后一次出手——导致战斗结束、胜负已分的那个瞬间,攻速慢的另一方的最后一次攻击显然是 尚未完成 的,因此应该直接舍弃掉结算。
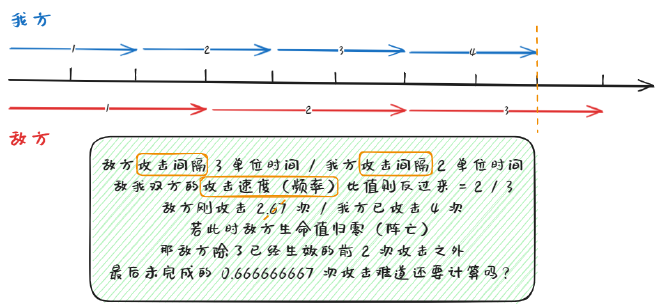
代入上面算出来的 公式1(我方 攻击次数 一式):
$$
\text{敌方攻击次数} n_2 = \left\lfloor \frac{\text{敌方攻击频率(攻击速度)} f_2}{\text{我方攻击频率(攻击速度)} f_1} \times \lceil \frac{\text{敌方总血量} HP_2}{\text{我方单次攻击伤害} DPS_1} \rceil \right\rfloor
$$
最后可得: $$ \text{我方战损} HP_1 = \text{敌方单次攻击伤害} DPS_2 \times \left\lfloor \frac{\text{敌方攻击频率(攻击速度)} f_2}{\text{我方攻击频率(攻击速度)} f_1} \times \lceil \frac{\text{敌方总血量} HP_2}{\text{我方单次攻击伤害} DPS_1} \rceil \right\rfloor $$
此处顺便引入简单的攻防系统,伤害计算公式: $$ \text{单次攻击伤害} DPS = \text{(攻击者的)攻击力} ATK - \text{(攻击目标的)防御力} DEF $$
如此一来,我们就得到了一个神奇的公式:
class BattleUnit {
constructor(name, health, attack, defense, attackSpeed = 1) {
this.name = name;
this.health = health;
this.attack = attack;
this.defense = defense;
this.attackSpeed = attackSpeed;
}
}
const hero = new BattleUnit("Hero", 100, 25, 10);
const enemy = new BattleUnit("Monster", 100, 20, 10);
hero.dps = hero.attack - enemy.defense;
enemy.dps = enemy.attack - hero.defense;
hero.attackConut = Math.ceil(enemy.health / hero.dps);
enemy.attackConut = Math.floor(
(enemy.attackSpeed / hero.attackSpeed) * hero.attackConut,
// 这里倒是真的有优化空间: 满足交换律的前提下 **先乘再除** 显然能够减少计算结果误差
// 两个整数乘不出浮点数 两个整数很容易除出浮点数 而浮点数就意味着 *近似值*
// 已经取过近似值的浮点数再乘以任何数(我知道 0 / 1 除外, 别杠)都相当于成倍放大误差
// 众所周知在 JS 中 0.1 + 0.2 !== 0.3
// BTW, *判断浮点数是否相等* 的正确姿势是 if (两数相减的差的绝对值 < 你最低能接受的精度误差值)
// Math.abs(0.1 + 0.2 - 0.3) < 0.0000000000000001
);
// 为了激励玩家 机制简单的游戏里一般会把敌人原本的攻击次数 -1 以表示玩家永远先出手(而不是比攻速)
// 否则本来以你的强度明明可以见面直接秒杀对方 结果进战后无论如何总得吃对面一下 还挺恶心的
// 伤害不高 侮辱性极强
const enemyDamage = enemy.dps * (enemy.attackConut - 1);
// 使用公式直接计算出战斗结果的时间复杂度显然为 O(1) 巧妙避开了真正模拟实时战斗的多轮计算
// 不过 作为代价也难以表现出战斗过程的细节 实际开发中需要根据设计目标自行权衡利弊做取舍
if (enemyDamage < hero.health) {
console.log(
`战斗结束,${hero.name} 击败了 ${
enemy.name
},自己受到了 ${enemyDamage} 点伤害,目前还剩余 ${
hero.health - enemyDamage
} 点 HP。`,
);
} else {
console.log(`战斗结束,${hero.name} 倒在了血泊中。`);
}
当然,你可以最后把这个公式的内容全部合并、写成一行,省掉 不必要 的中间变量以期减少(理论上的)内存使用量。
毕竟傻软 JavaScript 在绝大多数情况下 的赋值行为只会单纯地复制粘贴(而不是引用指针);
那只要多定义一个变量(哪怕只是 Number,哪怕只是临时),就得多占一点内存——整整他妈的 8 字节(64 位系统),你敢信?!
简直是他妈的骇人听闻惨绝人寰恶贯满盈天诛地灭的犯罪!是这个道理吧。
当然,你还得知道现代(你醒啦,已经是 4202 年了)的编译器 / 解释器乃至运行时——都不是傻子。
「中间代码优化」了解一下,「常数折叠 / 常数传播(此处不是但这东西确实存在)」了解一下,「tree shaking」了解一下,「自动垃圾回收」了解一下……过早 / 过度优化是一种病;而「声明变量」是开发过程中你最不应该去害怕的东西。
保证代码的可读性 比 提升人类压根都难以感知的那一丁点效率 的重要性不知高到哪里去了。
否则像 TypeScript 这种纯粹「画蛇添足」的玩意只要活着就是原罪,连呼吸都有错。(Turbo、Svelte 等的开发者:谁说不是呢?🤣)
你要真的 辣么 在乎效率,
效率比命都要重要,那你还写什么高级语言啊。
你知道所有 代码含有具体语义(以便人类理解)的编程语言 都叫「高级编程语言」吗?
因为它们通通都是经过高度封装的,运行源码需要进行大量转译工作(即编译过程);正常使用场景下哪怕你想、你都很难触及到底层实现。
如果真那么在乎效率,不如你直接写汇编好了,没有任何中间商(编译器 / 解释器 / 运行时)赚差价;
不,汇编都配不上你,你应该直接手写机器码——或者更干脆点,打 穿孔纸带 进行编程。
扩展研究#
本文只讨论了战斗中单挑(1v1)的情况,如果有大乱斗(多对多),会涉及到另一个非常有趣的概念。
它就是「兰彻斯特平方律」:简单来说,因为战斗单位阵亡的同时也意味着总体输出减少,优势方的「相对输出比」会像滚雪球般迅速扩大。这个优势的扩张速度(或者说劣势方的崩溃速度)不是线性的,而是平方级的。
核心原理——从中古开始,战斗单位就是有「生命值 / 血量(某种程度上也包含士气在内)」的,而不是简单地像下棋一样兑子(宏观来看,有时也确实会大道至简地回归到类似兑子的简略模型);伤害输出和受到的伤害都是平均分配的(数学期望平均,因为战争进程充满了随机性),火力弱、兵力少的一方受到「减员」的影响是必然急速扩大的链式反应。
正所谓——中国有句古话,叫识时务者为俊杰 兵败如山倒。
(咱们能用上的)具体应用场景:LOL 控兵线;至于 Dota 有「反补」和「拉野」可操作性和变数都会更多,LOL 就是纯纯的兰彻斯特方程。
再具体一点、比方说最简单的「推线」,你可以站在兵堆里 A 对方英雄吸引仇恨,对方小兵会转火 A 你;此时你的小兵仍然在 A 对方小兵,双方兵线原本相持不下的战斗力开始产生差距,兵线就推过去了。
不过这是短期结果,长期来看,由于兵线交汇点推进到了离对方基地更近的地方,对方后续支援的兵线会更快赶到战场形成更大规模的 局部以多打少,兰彻斯特平方律再次生效,于是己方兵线会更迅速地阵亡,之后对方兵线开始反推进,这就是「回推线」。加上对防御塔(的巨额伤害)的考量,因此是否选择把兵线推进塔(的攻击范围)里对「控线」来说非常重要。
当然了,对方英雄的行动(如果不是人机)由于背后玩家操作的存在,是完全混沌、不可预测(段位越低,反而越难预测 😂)的,这样就变成了动态博弈。这也是 PVP 游戏好玩的地方所在:与人斗,其乐无穷。如果双方的长线策略和临场抉择最后形成了纳什均衡,对线局面就会陷入胶着(「焦灼」感觉是误用),或者说「和平发育 (的垃圾时间)」。
篇幅有限,这里就不继续多做展开了,有机会再详细讨论(人话:咕)。
我们有缘再见。
